8.1 데이터를 분류하는 방법
이 절에서는 간단한 이차원 도형 정보를 다루어 보면서 데이터 유형이 필요한 이유와 데이터 유형을 관리하는 기초적인 방법을 알아본다.
8.1.1 개별 데이터 정의하기
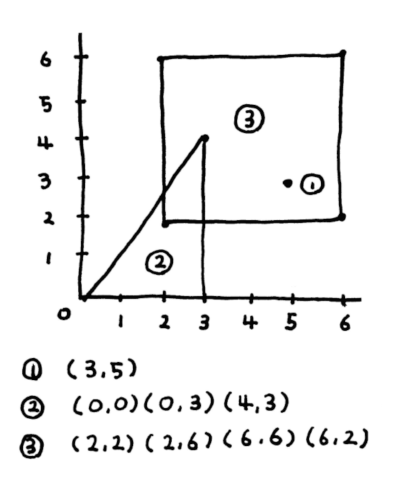
그림 8-1 좌표평면 위의 점과 도형
컬렉션을 중첩해서 복잡한 구조의 정보를 표현할 수 있다.(7.1절) 그림 8-1의 도형을 사전을 중첩하여 표현해 보자.
코드 8-1 좌표평면 위의 점과 도형
coordinate_1 = {'x': 5, 'y': 3} # ❶ 점 (좌표)
triangle_1 = { # ❷ 삼각형
'point_a': {'x': 0, 'y': 0}, # 삼각형의 각 꼭지점을
'point_b': {'x': 3, 'y': 0}, # 좌표로 나타냈다
'point_c': {'x': 3, 'y': 4},
}
rectangle_1 = { # ❸ 사각형
'point_a': {'x': 2, 'y': 2}, # 꼭지점이 네 개라서
'point_b': {'x': 6, 'y': 2}, # 좌표도 네 개다
'point_c': {'x': 6, 'y': 6},
'point_d': {'x': 2, 'y': 6},
}
❶ 점(좌표)은 x 축의 위치와 y 축의 위치가 쌍을 이루어 구성된다. 두 위치를 사전으로 묶자. ❷ 삼각형은 각 꼭지점의 위치를 나타내는 좌표 세 개를 묶은 사전으로 표현하자. ❸ 사각형도 마찬가지로 좌표 네 개를 묶은 사전으로 표현할 수 있다.
이렇게 나타낸 도형들의 둘레를 구하는 것도 가능하다. 두 점 사이의 거리를 구하는 함수를 정의하고, 그 함수를 이용해 도형의 둘레를 계산하는 함수를 정의하면 된다.
코드 8-2 두 점의 거리와 도형의 둘레를 계산하는 함수
import math # 제곱근(math.sqrt()) 계산을 위해 수학 모듈 임포트
def square(x):
"""전달받은 수의 제곱을 반환한다."""
return x * x
def distance(point_a, point_b):
"""두 점 사이의 거리를 계산해 반환한다. (피타고라스의 정리)"""
return math.sqrt(square(point_a['x'] - point_b['x']) +
square(point_a['y'] - point_b['y']))
def circumference_of_triangle(shape):
"""삼각형 데이터를 전달받아 둘레를 구해 반환한다."""
a_to_b = distance(shape['point_a'], shape['point_b'])
b_to_c = distance(shape['point_b'], shape['point_c'])
c_to_a = distance(shape['point_c'], shape['point_a'])
return a_to_b + b_to_c + c_to_a
def circumference_of_rectangle(shape):
"""사각형 데이터를 전달받아 둘레를 구해 반환한다."""
a_to_b = distance(shape['point_a'], shape['point_b'])
b_to_c = distance(shape['point_b'], shape['point_c'])
c_to_d = distance(shape['point_c'], shape['point_d'])
d_to_a = distance(shape['point_d'], shape['point_a'])
return a_to_b + b_to_c + c_to_d + d_to_a
# 둘레 계산
print(circumference_of_triangle(triangle_1)) # 12.0
print(circumference_of_rectangle(rectangle_1)) # 16.0
실행 결과:
12.0
16.0
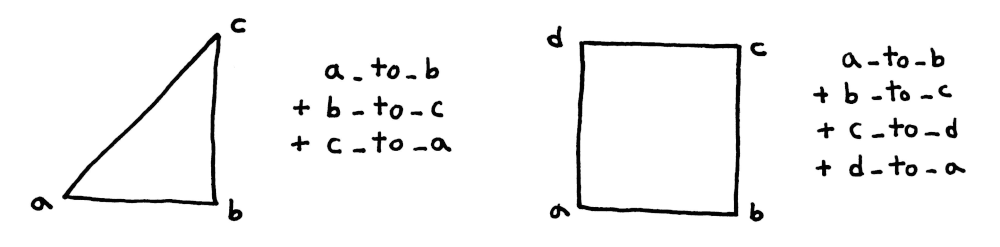
그림 8-2 도형의 둘레를 구하는 방법
도형 데이터를 잘 표현했고, 도형들의 둘레도 정확히 구할 수 있게 되었다. 위치나 크기가 다른 삼각형이나 사각형을 정의하고 위 함수로 둘레를 계산할 수도 있을 것이다.
8.1.2 개별 데이터를 정의하기 위한 유형을 약속하기
데이터를 단 하나만 정의하고 사용할 때는 상관이 없지만, 동일한 범주의 데이터를 여럿 정의할 때는 문제가 생길 수 있다. 컬렉션을 활용해 복잡한 데이터 구조를 나타낼 때, 그 구조를 쌓아올리는 방식이 여러 가지일 수 있기 때문이다. 그림 8-1의 도형들을 코드 8-2와는 다른 구조로 표현할 수도 있다.
코드 8-3 좌표평면 위의 점과 도형 (다른 표현)
coordinate_2 = (3, 5) # ❶ 점 (좌표)
triangle_2 = ((0, 0), (0, 3), (4, 3)) # ❷ 삼각형
rectangle_2 = { # ❸ 사각형
'point': (2, 2),
'width': 4,
'height': 4,
}
❶ 좌표를 사전 대신 (y, x) 형태의 튜플로 표현했다. ❷ 삼각형은 좌표의 튜플로 표현했다. ❸ 사각형은 기준점이 되는 좌표(point)와 넓이(width)·높이(height)를 갖는 사전으로 표현했다.
이처럼 대상을 나타내는 데 필요한 정보를 모두 담을 수만 있다면, 데이터를 담는 구조는 자유롭게 구성할 수 있다. 그런데 데이터의 구조가 달라지면 데이터를 처리하는 방법도 달라진다는 것이 문제다. 코드 8-1과 코드 8-3은 같은 정보를 나타내지만, 데이터의 구조가 서로 달라 동일한 방법으로 처리할 수가 없다.
코드 8-4 데이터의 표현 방식이 다르면 같은 함수를 사용할 수 없다
print(circumference_of_triangle(triangle_2))
# TypeError: tuple indices must be integers or slices, not str
코드 8-2에서 정의한 함수로 코드 8-3으로 작성한 도형의 둘레를 계산하려 하면 오류가 발생한다.
주석으로 데이터의 유형·구조 약속하기
이 문제를 해결하기 위해서는 데이터 객체들(개별 도형들)을 제각각 생각하는 것이 아니라, 데이터 유형(삼각형, 사각형 등)이라는 범주로 묶어 생각할 수 있어야 한다. 동일한 범주에 속하는 데이터의 유형을 정의하고 그 구조를 동일하게 구성하는 것이다. 지금 우리가 다루고 있는 정보의 범주는 좌표·삼각형·사각형이다. 이들의 유형과 구조를 약속해 보자. 아직 데이터 유형을 정의하는 파이썬 문법을 모르므로, 주석을 이용한다.
코드 8-5 데이터 유형마다 구조를 주석으로 정해 놓기
# 유형: '좌표'는 다음 키를 갖는 사전이다.
# * 'x': x 축의 위치 (정수)
# * 'y': y 축의 위치 (정수)
coordinate_1 = {'x': 5, 'y': 3}
# 유형: '삼각형'은 다음 키를 갖는 사전이다.
# * 'point_a': 첫번째 점의 위치 (좌표)
# * 'point_b': 두번째 점의 위치 (좌표)
# * 'point_c': 세번째 점의 위치 (좌표)
triangle_1 = {
'point_a': {'x': 0, 'y': 0},
'point_b': {'x': 3, 'y': 0},
'point_c': {'x': 3, 'y': 4},
}
# 유형: '사각형'은 다음 키를 갖는 사전이다.
# * 'point_a': 첫번째 점의 위치 (좌표)
# * 'point_b': 두번째 점의 위치 (좌표)
# * 'point_c': 세번째 점의 위치 (좌표)
# * 'point_d': 네번째 점의 위치 (좌표)
rectangle_1 = {
'point_a': {'x': 2, 'y': 2},
'point_b': {'x': 6, 'y': 2},
'point_c': {'x': 6, 'y': 6},
'point_d': {'x': 2, 'y': 6},
}
이렇게 약속을 정해 두면, 삼각형과 사각형을 여러 개 정의하더라도 모두 같은 구조로 정의할 수 있을 것이다. 그리고 모두 코드 8-2의 함수로 둘레를 계산할 수 있을 것이다.
개념 정리
- 동일한 범주의 정보라 하더라도 서로 다른 구조로 표현할 수 있다.
- 어떤 범주의 데이터에 통용되는 연산(함수)을 준비하기 위해서는 데이터의 유형과 구조를 정해두어야 한다.
연습문제
연습문제 8-1 체스말, 바둑돌 정의하기
다음은 사전을 이용해 체스말과 바둑돌 데이터를 나타낸 예다. 체스 말 데이터에서 ‘x’, ‘y’가 위치, ‘color’가 색, ‘role’이 역할을 나타낸다. 바둑돌 데이터에서는 ‘x’, ‘y’가 돌의 위치, ‘order’가 몇 수째에 둔 것인지를 뜻하는 수, ‘color’가 돌의 색을 나타낸다.
# 이곳에 체스말 데이터 유형 정의하기
체스말1 = {'x': 'A', 'y': '8', 'color': 'black', 'role': '룩'}
체스말2 = {'x': 'E', 'y': '1', 'color': 'white', 'role': '킹'}
# 이곳에 바둑돌 데이터 유형 정의하기
바둑돌1 = {'x': 8, 'y': 14, 'order': 83, 'color': '흑'}
바둑돌2 = {'x': 12, 'y': 3, 'order': 84, 'color': '백'}
이 프로그램을 수정하여 체스말 데이터 유형과 바둑돌 데이터 유형을 주석으로 정의해 보아라.
8.1.3 데이터의 유형 구별하기
코드 8-2에서는 삼각형의 둘레를 구하는 circumference_of_triangle() 함수와 사각형의 둘레를 구하는 circumference_of_rectangle() 함수를 각각 정의했다. 그런데 이 함수는 둘 다 ‘도형의 둘레’를 구하는 함수다. 다른 점은 계산하려는 대상의 유형 뿐이다. 함수 이름에 _of_triangle(삼각형의)와 같이 도형의 종류가 붙고 있어서 함수 이름이 너무 길어진다. 도형의 유형이 늘어날 때마다 비슷한 함수를 계속 만들어야 하는 문제도 있다. circumference()(둘레)라는 함수를 하나 정의해두고, 이 함수로 여러 가지 도형의 둘레를 구할 수 있다면 편리하지 않을까?
인자의 유형에 따라 다르게 동작하는 함수
이 함수를 만들려면 if 문을 이용해 함수가 전달된 인자의 유형에 따라 다른 동작을 하도록 하면 된다. 데이터의 유형은 type() 함수(4.5절)를 이용하여 확인할 수 있다. if 문과 type() 함수를 이용해 코드 8-2의 circumference_of_triangle() 함수와 circumference_of_rectangle() 함수를 하나로 합쳐 보자.
코드 8-6 둘레 계산 함수를 일반 함수로 정의하기 (잘못된 방법)
def circumference(shape):
"""도형 데이터를 전달받아 둘레를 구해 반환한다."""
if type(shape) == '삼각형': # ❶ 도형의 데이터 유형이 '삼각형'인 경우
a_to_b = distance(shape['point_a'], shape['point_b'])
b_to_c = distance(shape['point_b'], shape['point_c'])
c_to_a = distance(shape['point_c'], shape['point_a'])
return a_to_b + b_to_c + c_to_a
elif type(shape) == '사각형': # ❷ 도형의 데이터 유형이 '사각형'인 경우
a_to_b = distance(shape['point_a'], shape['point_b'])
b_to_c = distance(shape['point_b'], shape['point_c'])
c_to_d = distance(shape['point_c'], shape['point_d'])
d_to_a = distance(shape['point_d'], shape['point_a'])
return a_to_b + b_to_c + c_to_d + d_to_a
else: # ❸ 지원하지 않는 유형인 경우
return None
# ❹ 잠깐! 삼각형과 사각형을 함수에 대입해보면, 의도와 달리 None이 반환된다!
print(circumference(triangle_1)) # None
print(circumference(rectangle_1)) # None
실행 결과:
None
None
❶, ❷에서 type() 함수를 이용해 데이터의 유형을 판단하고, 그에 따라 둘레를 다른 방법으로 계산하도록 했다. 그런데 함수를 호출하면 삼각형을 입력하든 사각형을 입력하든, None이 반환될 뿐이다. 그 이유는 ❶ type(triangle_1)과 ❷ type(rectangle_1)의 평가 결과가 삼각형과 사각형이 아니기 때문이다. 기억하는가? 우리는 삼각형 유형과 사각형 유형을 주석으로만 정의해두었다. 컴퓨터는 주석을 무시하므로, 당연히 우리의 데이터 유형 정의를 이해하지 못한다.
코드 8-7 삼각형과 사각형 데이터 둘 다 유형이 ‘사전’이다
print(type(triangle_1)) # <class 'dict'>
print(type(rectangle_1)) # <class 'dict'>
데이터의 유형을 나타내는 정보 추가하기
type() 함수를 사용할 수 없다면 데이터의 유형을 어떻게 구별할 수 있을까? 데이터 유형에 해당되는 정보를 추가하면 되지 않을까? 사전으로 정의한 도형 데이터 속에 'type'이라는 키를 새로 추가하고, 이 키의 값을 데이터 유형으로 사용하자.
코드 8-8 데이터 유형을 나타내는 정보를 사전에 추가하기
triangle_3 = {
'type': '삼각형', # 데이터의 유형을 나타내는 정보
'point_a': {'x': 0, 'y': 0},
'point_b': {'x': 3, 'y': 0},
'point_c': {'x': 3, 'y': 4},
}
rectangle_3 = {
'type': '사각형', # 데이터의 유형을 나타내는 정보
'point_a': {'x': 2, 'y': 2},
'point_b': {'x': 6, 'y': 2},
'point_c': {'x': 6, 'y': 6},
'point_d': {'x': 2, 'y': 6},
}
이제 도형 데이터의 'type' 키를 조사하면 데이터의 유형을 구할 수 있다. 코드 8-6의 둘레 계산 함수를 다음과 같이 수정하고, type 키가 들어있는 도형 데이터를 입력하여 실행하면 함수가 올바르게 동작한다.
코드 8-9 둘레 계산 함수를 일반 함수로 정의하기 (수정된 방법)
def circumference(shape):
"""도형 데이터를 전달받아 둘레를 구해 반환한다."""
if shape['type'] == '삼각형': # type() 함수 대신 인덱싱 연산 사용
a_to_b = distance(shape['point_a'], shape['point_b'])
b_to_c = distance(shape['point_b'], shape['point_c'])
c_to_a = distance(shape['point_c'], shape['point_a'])
return a_to_b + b_to_c + c_to_a
elif shape['type'] == '사각형': # type() 함수 대신 인덱싱 연산 사용
a_to_b = distance(shape['point_a'], shape['point_b'])
b_to_c = distance(shape['point_b'], shape['point_c'])
c_to_d = distance(shape['point_c'], shape['point_d'])
d_to_a = distance(shape['point_d'], shape['point_a'])
return a_to_b + b_to_c + c_to_d + d_to_a
else:
return None
print(circumference(triangle_3)) # 12.0
print(circumference(rectangle_3)) # 16.0
실행 결과:
12.0
16.0
이와 같이 데이터의 구조에 데이터의 유형 자체를 나타내는 정보를 추가함으로써 데이터의 유형을 구별하는 것이 가능해진다. 함수가 데이터의 유형을 참고하여 그에 맞게 동작하도록 하는 것도 가능하다.
개념 정리
- 데이터에 데이터의 유형을 나타내는 정보를 추가할 수 있다.
- 데이터의 유형을 구별할 수 있으면 그에 따라 알맞는 연산을 수행할 수 있다.
연습문제
연습문제 8-2 체스말, 바둑돌 출력하기
연습문제 8-1에서 정의한 체스말 또는 바둑돌 데이터를 전달받아 화면에 출력하는 함수 print_piece()를 정의해라. 이 함수는 전달받은 데이터가 체스말인지, 바둑돌인지를 식별해 각각 다른 방식으로 출력해야 한다. 다음은 이 함수를 실행한 예다.
>>> print_piece(체스말1)
black 룩이 A8 위치에 놓여 있어요.
>>> print_piece(바둑돌2)
제 84 수: 백이 (12, 3) 위치에 두었습니다.
8.1.4 이걸로 충분할까?
이 절에서 배운 기법을 활용하면 데이터들을 범주에 따라 여러 가지 유형으로 분류하여 다룰 수 있을 것이다. 하지만 아직 적셔야 할 목마름이 있다.
첫번째, 데이터의 유형을 정의할 때 주석을 이용하는 것보다는 파이썬의 기능을 이용하는 편이 좋다. 그러면 컴퓨터도 데이터 유형을 인식할 수 있고, type() 함수로 유형을 식별하는 것도 가능할 것이다. 그 방법은 8.2절과 8.3절에서 알아본다.
두번째, 데이터 유형에 알맞는 함수를 지정하는 방법이 적절하지 않다. 일반 함수를 정의함으로써 여러 개의 함수를 정의하지 않아도 되는 점은 편리해졌지만, 함수 하나에 다양한 유형의 계산 방법을 넣어둔 것은 바람직하지 않다. (데이터 유형이 많아질수록 함수가 길고 복잡해질 테니까!) 각 데이터 유형마다 그에 맞는 함수를 별도로 정의하되, 그 함수가 그 데이터 유형에 대해서만 실행될 수 있도록 강제하는 편이 좋다. 그 방법은 8.3절과 8.5절에서 알아볼 것이다.
댓글 남기기