5.4 집합
‘카페인이 든 음료들’이라는 컬렉션과 ‘가격이 3천 원 이하인 음료들’이라는 컬렉션에 모두 포함되어 있는 음료(교집합)는 어떻게 구할 수 있을까? 또 ‘카페 라테’가 그 속에 포함되는지(소속 검사)는 어떻게 알 수 있을까? 시퀀스나 매핑을 이용해서도 구할 수 있지만, 집합(set)을 이용하면 이런 문제를 더 쉽고 빠르게 해결할 수 있다.
5.4.1 원소를 묶어 둔 데이터 구조
집합은 그 속에 포함되어야 할 원소들을 묶어 놓은 데이터 구조다. 학교 수학 시간에 배우는 바로 그 집합에서 따온 것이기 때문에, 수학의 집합과 거의 비슷한 특징을 가진다. 두 집합의 합집합, 교집합, 차집합 같은 집합 연산도 할 수 있고, ‘카페 라테’가 어떤 집합에 포함되어 있는지 소속 검사도 할 수 있다.
데이터를 모아 둔 컬렉션이라는 점에서 집합은 다른 컬렉션(특히 시퀀스)과 비슷해 보이지만, 차이점이 있다. 집합은 원소에 순서(번호)나 키를 붙여 관리하지 않는다. 그저 포함해야 할 원소를 원소를 담고 있을 뿐이다. 또, 시퀀스와 매핑은 동일한 값을 여러 개 중복으로 저장할 수 있지만 집합은 동일한 원소는 하나만 가질 수 있다. 그래서 어떤 원소가 집합에 포함되는지는 알 수 있어도, 그 원소가 몇 번째인지 또는 몇 개나 있는지는 알 수 없다.
집합의 특징
- 순서나 키 없이, 포함되는 원소를 모아 둔 데이터 구조다.
- 원소를 중복으로 저장하지 않는다.
- 합집합, 교집합 같은 수학의 집합 연산이 가능하다.
- 어떤 원소가 집합에 포함되었는지 검사할 수 있다.
5.4.2 집합 표현하기
파이썬에서 집합을 표현하고 정의하는 양식은 리스트의 표현 양식과 거의 똑같다. {1, 2, 3, 4}와 같이 중괄호({})를 이용해 데이터를 묶고, 각 원소를 쉼표로 구분한다. 대괄호 대신 중괄호로 감싼다는 점만 리스트와 다르다. 중괄호는 {키1: 값1, 키2: 값2}와 같이 사전을 표현하는 양식에도 사용되는데, 사전은 콜론(:)으로 표현된 키-값 쌍을 담기 때문에 집합의 양식과 차이가 있다.
단, 공집합(원소가 없는 집합)은 중괄호로 표현할 수 없다. 빈 중괄호 표현({})은 빈 집합이 아니라 빈 사전을 표현하는 것으로 약속되어 있다. 공집합은 set()으로 나타낸다.
-
원소가 하나인 집합
{원소1, 원소2, 원소3, …}
-
공집합
set()
이 양식에 따라, 대화식 셸에서 몇 가지 집합을 표현해 보자.
코드 5-60 집합 표현하기
# 정수의 집합
{0, -127, 97, 1789}
# 이메일 주소의 집합
{'bakyeono@gmail.com', 'i@bakyeono.net'}
# 공집합
set()
연습문제
연습문제 5-13 집합 정의하기
다음 세 집합을 각각 파이썬 코드로 정의하라.
* 한 주의 모든 요일
* 여러분이 학교나 직장에 가는 요일
* 여러분이 휴식을 취하는 요일
5.4.3 시퀀스를 집합으로 변환하기
시퀀스는 순서와 중복이 있다는 점을 제외하면 집합과 형태가 유사하다. 따라서 집합을 시퀀스로 변환하거나 반대로 집합을 시퀀스로 변환할 수 있다. 단, 시퀀스를 집합으로 변환할 때는 원소의 순서와 중복된 원소가 사라진다는 점에 유의해야 한다.
시퀀스를 집합으로 변환할 때는 set() 함수를 사용한다.
코드 5-61 시퀀스를 집합으로 변환하기
>>> set([6, 1, 1, 2, 3, 3, 1, 5, 5, 4]) # 리스트를 집합으로
{1, 2, 3, 4, 5, 6}
>>> set(('사과', '토마토', '바나나', '감')) # 튜플을 집합으로
{'감', '사과', '바나나', '토마토'}
위 코드에서 확인할 수 있듯, 시퀀스를 집합으로 변환하면 중복된 원소는 하나만 남고, 원소의 순서는 유지되지 않는다.
레인지를 정의한 후 집합으로 변환하면, ‘0 이상 1만 미만의 모든 짝수’와 같은 일정 범위의 규칙적인 수의 집합을 쉽게 생성할 수 있다.
코드 5-62 레인지를 이용해 집합 정의하기
>>> 짝수 = set(range(0, 10000, 2))
>>> 홀수 = set(range(1, 10000, 2))
집합의 원소가 될 수 있는 데이터
집합은 수, 문자열, 불리언, 튜플, 레인지 등의 불변 데이터를 원소로 가질 수 있다. 하지만 리스트나 사전 같은 가변 데이터, 그리고 가변 데이터를 담은 튜플은 집합의 원소가 될 수 없다.
시퀀스에서 중복된 원소 제거하기
시퀀스의 중복 원소를 제거할 때 집합 변환을 활용할 수 있다. 시퀀스를 집합으로 변환했다가 다시 시퀀스로 변환하면 된다.
코드 5-63 리스트에서 중복 원소 제거하기
>>> list(set([6, 1, 1, 2, 3, 3, 1, 5, 5, 4]))
[1, 2, 3, 4, 5, 6]
단, 이 방법을 사용할 때는 중복 원소뿐 아니라 원소의 순서라는 중요한 정보가 함께 사라진다는 점에 유의해야 한다.
연습문제
연습문제 5-14 중복 없이 시퀀스 합치기
0 이상 1000 미만의, 3의 배수 또는 4의 배수는 모두 몇 개인지 계산하라.
힌트: 레인지, 리스트, 집합을 모두 활용하자.
5.4.4 집합 연산
집합은 소속 검사, 합집합, 교집합, 여집합, 차집합, 부분집합 검사 등 수학의 집합 연산을 수행할 수 있다. 대화식 셸에서 직접 코드를 입력하며 집합 연산을 학습해 보자. 연습에 사용할 집합을 다음과 같이 정의하자.
코드 5-64 집합의 원소 개수 세기
>>> 들짐승 = {'사자', '박쥐', '늑대', '곰'}
>>> 날짐승 = {'독수리', '매', '박쥐'}
>>> 바다생물 = {'참치', '상어', '문어 괴물'}
원소 개수 세기
시퀀스, 매핑에서 요소의 개수를 세는 len() 함수는 집합의 원소 개수를 셀 때도 똑같이 사용된다.
코드 5-65 집합의 원소 개수 세기
>>> len(들짐승)
4
소속 검사하기
어떤 원소를 포함하는지 확인하는 것은 집합의 핵심 기능이다. 시퀀스에서 요소를 검사할 때, 그리고 매핑에서 키를 검사할 때처럼 in과 not in 예약어를 이용해 원소를 검사할 수 있다.
코드 5-66 집합에서 소속 검사하기
>>> '늑대' in 들짐승
True
>>> '곰' not in 들짐승
False
집합의 소속 검사와 시퀀스의 소속 검사
요소의 소속을 검사하는 기능은 시퀀스에도 있다. 예를 들어,
'늑대' in list(들짐승)과 같이 리스트에서 소속을 검사하더라도 연산 결과는 집합에서와 똑같다.하지만 실제로 이루어지는 검사 과정에 차이가 있다. 시퀀스의 소속 검사 기능은 요소를 처음부터 끝까지 순서대로 하나씩 확인하면서 찾는다. 반면, 집합은 해시 알고리즘이라는 방법을 사용하기 때문에 데이터의 양이 적든 많든 언제나 소속 검사를 단 번에 수행해 낸다. 그래서 컬렉션에 저장된 데이터의 양이 많을 수록 시퀀스보다는 집합의 검사 방식이 유리하다.
그렇다면 시퀀스에서 소속 검사를 할 때는 먼저 집합으로 변환해야 할까? 그렇지는 않다. 시퀀스를 집합으로 변환하는 데도 연산 비용이 들기 때문이다. 시퀀스에서 원소를 검사할 때는 그냥 시퀀스인 상태로 검사하는 편이 낫다. 하지만 검사를 자주 수행해야 하는 데이터 컬렉션을 정의할 때는 집합으로 정의하는 것을 고려해 보자.
집합에서 특정 원소 구하기?
집합은 원소의 순서나 키를 관리하지 않으므로 당연히 인덱싱 연산도 지원하지 않는다. 따라서 들짐승[0] 이나 들짐승['늑대'] 같은 표현은 오류다. 집합에서 어떤 원소를 구한다는 것은 그 원소가 포함되어 있는지를 확인한다는 의미밖에 없다.
합집합 구하기
합집합(union)은 두 집합의 모든 원소를 합한 집합이다.
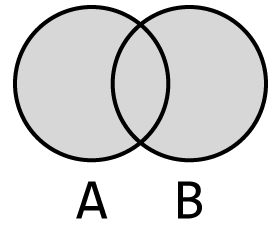
그림 5-7 A와 B의 합집합
합집합은 union(다른집합) 메서드를 사용하여 구할 수 있다.
코드 5-67 두 집합의 합집합 구하기
>>> 짐승 = 들짐승.union(날짐승) # 들짐승과 날짐승의 합집합
>>> 짐승
{'곰', '사자', '박쥐', '늑대', '독수리', '매'}
합집합은 | 연산자로도 구할 수 있다.
코드 5-68 | 연산자로 합집합 구하기
>>> 들짐승 | 날짐승
{'곰', '사자', '박쥐', '늑대', '독수리', '매'}
>>> 들짐승 | 날짐승 | {'인간'} # ❶ 여러 집합을 연달아 합할 때
{'곰', '사자', '박쥐', '늑대', '인간', '독수리', '매'}
❶과 같이 여러 집합을 연달아 합할 때 | 연산자를 사용하면 편리하다.
교집합 구하기
교집합(intersection)은 두 집합이 공통으로 포함하는 모든 원소의 집합이다.
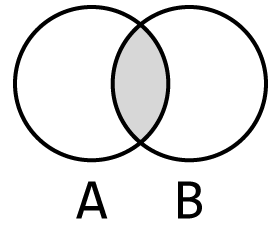
그림 5-8 A와 B의 교집합
교집합은 intersetion(다른집합) 메서드를 사용하여 구할 수 있다.
코드 5-69 두 집합의 교집합 구하기
>>> 들짐승.intersection(날짐승) # 들짐승과 날짐승의 교집합
{'박쥐'}
>>> 들짐승.intersection(바다생물) # 짐승과 바다생물의 교집합
set()
교집합은 & 연산자로도 구할 수 있다.
코드 5-70 & 연산자로 교집합 구하기
>>> 들짐승 & 날짐승
{'박쥐'}
차집합 구하기
차집합(difference set)은 한 집합에서 다른 집합에 존재하는 모든 원소를 뺀 집합이다.
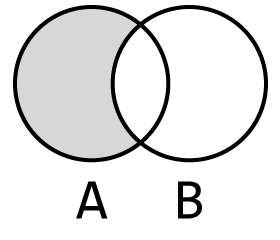
그림 5-9 A에서 B를 뺀 차집합
차집합은 difference(다른집합) 메서드를 사용하여 구할 수 있다.
코드 5-71 차집합 구하기
>>> 짐승.difference(날짐승) # 짐승에서 날짐승을 뺀 집합
{'곰', '사자', '늑대'}
차집합은 - 연산자로도 구할 수 있다.
코드 5-72 - 연산자로 차집합 구하기
>>> 날짐승 - 들짐승 # 날짐승에서 들짐승을 뺀 집합
{'독수리', '매'}
대칭차 구하기
대칭차(symmetric difference)는 두 집합의 합집합에서 교집합을 뺀 것이다. 즉, 두 집합이 함께 갖지 않은 모든 원소의 집합이다.
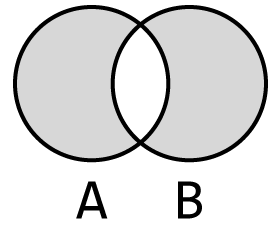
그림 5-10 A와 B의 대칭차
대칭차는 symmetric_difference(다른집합) 메서드를 사용하여 구할 수 있다.
코드 5-73 두 집합의 대칭차 구하기
>>> 들짐승.symmetric_difference(날짐승) # 들짐승과 날짐승의 대칭차
{'사자', '늑대', '곰', '독수리', '매'}
대칭차는 ^ 연산자로도 구할 수 있다.
코드 5-74 ^ 연산자로 대칭차 구하기
>>> 들짐승 ^ 날짐승 # 들짐승과 날짐승의 대칭차
{'사자', '늑대', '곰', '독수리', '매'}
부분집합 검사하기
집합 B의 모든 원소가 집합 A에 포함되어 있으면, 집합 B는 집합 A의 부분집합(subset)이다.
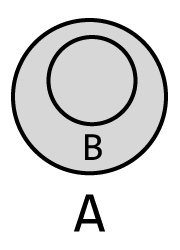
그림 5-11 B는 A의 부분집합
한 집합이 다른 집합의 부분집합인지 검사할 때는 issubset(다른집합) 메서드를 사용한다.
코드 5-75 부분집합 검사하기
>>> 들짐승.issubset(짐승) # 들짐승이 짐승의 부분집합인가?
True
>>> 들짐승.issubset(날짐승) # 들짐승이 날짐승의 부분집합인가?
False
부분집합은 비교 연산자(<=)로도 구할 수 있다.
코드 5-76 부분집합 검사하기
>>> 들짐승 <= 짐승
True
>>> 들짐승 <= 날짐승
False
부분집합의 반대인 상위집합(superset)이라는 개념도 있다. 상위집합을 검사할 때는 issuperset() 메서드 또는 >= 연산자를 사용할 수 있다.
서로소 집합 검사하기
집합 A와 집합 B에 공통된 원소가 하나도 없으면, 두 집합은 서로소 집합(disjoint set)이다.
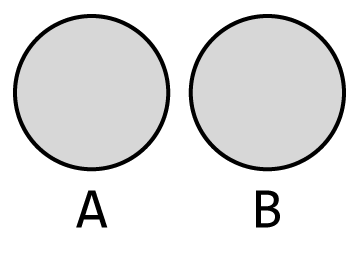
그림 5-12 A와 B는 서로소 집합
서로소 집합을 검사하려면 isdisjoint(다른집합) 메서드를 사용한다.
코드 5-77 서로소 집합 검사하기
>>> 들짐승.isdisjoint(날짐승)
False
>>> 들짐승.isdisjoint(바다생물)
True
원소 변경하기
집합은 수정 가능한 데이터다. 이미 정의한 집합에 원소를 추가하거나 삭제할 수 있다. 다음과 같은 메서드를 사용한다.
add(데이터): 데이터를 원소로 추가discard(원소): 원소 제거remove(원소): 원소 제거 (원소가 없으면 오류)pop(): 아무 원소나 꺼낸다 (집합이 비어있으면 오류)clear(): 모든 원소를 제거
대화식 셸에서 메서드를 사용해 보자.
코드 5-78 집합 원소 수정하기
>>> 들짐승.add('인간') # 들짐승에 인간 추가
>>> 들짐승
{'사자', '늑대', '곰', '인간', '박쥐'}
>>> 들짐승.discard('인간') # 인간 제거
>>> 들짐승
{'사자', '늑대', '곰', '박쥐'}
>>> 들짐승.remove('곰') # 곰 제거
>>> 들짐승
{'사자', '늑대', '박쥐'}
>>> 들짐승.pop() # 아무 원소나 꺼내기
'사자'
>>> 들짐승
{'늑대', '박쥐'}
>>> 들짐승.clear() # 모든 원소 제거
>>> 들짐승
set()
이상으로 집합으로 수행할 수 있는 다양한 연산을 알아보았다. 수학의 집합론은 프로그래밍에서도 자주 활용되는 개념이다. 어떤 문제를 해결하는 데 집합 연산이 필요하다면 파이썬의 집합 연산을 활용해 계산할 수 있다.
연습문제
연습문제 5-15 일하는 날
is_working_day() 함수를 정의하라. 이 함수는 요일을 입력받아 그 요일이 여러분이 쉬는 날이면 True, 아니면 False를 반환한다.
연습문제 5-16 집합 계산 1
0 이상 1000 미만의, 3과 4의 공배수는 모두 몇 개인지 계산하라.
연습문제 5-17 집합 계산 2
0 이상 1000 미만의, 3의 배수이되 4의 배수는 아닌 수는 모두 몇 개인지 구하라.
5.4.5 프로즌셋
집합은 리스트, 사전처럼 수정이 가능한 데이터다. 한 번 집합을 정의한 뒤에도 원소를 추가, 삭제할 수 있다.
수정이 불가능한 집합 컬렉션을 정의하고 싶다면 프로즌셋(frozenset)을 사용하면 된다. 프로즌셋을 정의하는 방법은 다음과 같다.
- 공집합 프로즌셋:
frozenset() - 집합에서 정의하기:
frozenset({원소 1, 원소 2, 원소 3, ...}) - 시퀀스에서 정의하기:
frozenset([원소 1, 원소 2, 원소 3, ...])
프로즌셋은 집합과 사용 방법이 거의 동일하고 연산과 메서드도 공유한다. 단, 내용을 수정하는 연산과 메서드는 지원하지 않는다. 프로즌셋이 필요한 경우는 거의 모두 집합으로 대체 가능하여 자주 사용되지는 않는다. 이런 것이 있다는 것만 알아 두자.
댓글 남기기