2.1 수식 계산
파이썬을 일종의 고급 계산기처럼 사용할 수 있다. 파이썬 코드로 다양한 계산식을 표현할 수 있고, 컴퓨터는 이 식을 그대로 계산해 준다. 이 절에서는 다양한 수식을 파이썬으로 계산해 본다. 수식이라고 하면 어렵게 들릴 수 있으나 간단한 사칙연산과 부등식 정도이니 걱정하지 않아도 된다.
2.1.1 수식 나타내고 계산하기
파이썬에서 수식을 계산하는 건 어렵지 않다. 1장에서 해 본 것처럼, 파이참을 실행하고 대화식 셸에 수식을 입력하면 된다. (>>> 이라는 입력 표시가 나와 있는 코드는 모두 대화식 셸에서 입력하는 예제다. 대화식 셸의 예제는 여러분도 직접 따라 입력해보는 것이 좋다. 샵 기호(#) 뒤의 내용은 주석이므로 입력하지 않아도 된다.)
코드 2-1 간단한 수식 계산
>>> 1917 - 2017
-100
>>> 32 * 3.1415 # 별 기호(*)는 곱셈을 의미
100.528
>>> 90 / 360 # 빗금 기호(/)는 나눗셈을 의미
0.25
코드 2-1에서 확인할 수 있듯이 대화식 셸에 수식을 입력하면 바로 계산되어 결과가 출력된다.
파이썬에서 수식을 표기하고 계산하는 방법은 수학과 거의 비슷하다. 다른 점은 곱셈에 별 기호(*)를, 나눗셈에 빗금 기호(/)를 사용한다는 점이다. 곱셈과 나눗셈을 계산할 때 유의하자.
잠깐, 파이참이 뭐지? 대화식 셸은 또 뭐야?
파이참은 파이썬 프로그래밍을 위한 개발 도구 프로그램이다. 대화식 셸은 파이썬 프로그램 파일을 작성하지 않고도 한 행씩 명령을 바로 실행하며 결과를 확인할 수 있는 도구다. 파이참 상단 메뉴에서 ‘Tools -> Python Console…‘를 클릭하여 실행할 수 있다.
잘 모르겠으면 1장을 다시 살펴보자.
연산자
덧셈 기호(+), 뺄셈 기호(-)처럼 수를 어떻게 계산해야 하는지 알려주는 기호를 연산자라고 부른다. 파이썬에는 사칙연산을 비롯한 여러 가지 연산자가 있다.
| 연산자 | 의미 |
|---|---|
+ |
덧셈 |
- |
뺄셈 |
* |
곱셈 |
/ |
나눗셈 |
** |
거듭제곱 |
// |
몫 |
% |
나머지 |
표 2-1 수의 계산을 위한 연산자
표 2-1에 나온 연산자들을 살펴보자. 덧셈, 뺄셈, 곱셈, 나눗셈이야 모르는 사람이 없다. 하지만 거듭제곱, 몫, 나머지를 구하는 연산자는 생소할 것이다. 어떻게 동작하는지 대화식 셸에 입력해 알아보자.
코드 2-2 거듭제곱
>>> 2 ** 8 # 2의 8승
256
>>> 10 ** 20 # 10의 20승
100000000000000000000
>>> 9999 ** 9999 # 9999의 9999승
3678978362165515792692625984783565804550254...(결과 생략)
보다시피 사람은 감당하기 힘든 거듭제곱도 컴퓨터는 순식간에 계산해 낸다.
이번에는 나눗셈, 몫, 나머지를 비교해 보자.
코드 2-3 나눗셈, 몫, 나머지
>>> 100 / 3 # 나눗셈 연산자는 소수점 아래의 작은 단위까지 구해 준다
33.333333333333336
>>> 100 // 3 # 몫 연산자는 몫만 구하고 소수점 아래 자리는 버린다
33
>>> 100 % 3 # 나머지 연산자를 이용하면 남은 수를 구할 수 있다
1
빨셈 기호(-)는 뺄셈 연산자로도 쓰이지만, 수의 부호를 바꿀 때도 쓰인다. 뺄셈 기호 왼쪽에 수(피연산자)가 없고 오른쪽에만 수가 있으면, 그 수의 부호를 바꾼다.
코드 2-4 부호 바꾸기 연산
>>> - 100 # -는 수의 부호를 바꾼다
-100
>>> - - 100 # 부호를 두 번 바꾸면 원래 수가 된다
100
지금 소개한 연산자는 모두 수의 계산에 관련된 산술 연산자다. 산술 연산자 외에도 변수에 값을 대입하는 대입 연산자, 두 값을 비교하는 비교 연산자, 조건식을 연결하는 논리 연산자 등이 있다. 이들에 대해서도 곧 배울 것이다.
연산자가 여러 개일 때의 연산 순서
수식에서는 여러 개의 연산자가 중첩될 수 있고, 얼마든지 많아질 수도 있다. 수식이 길고 복잡해도 하나씩 계산해 나가면 된다. 이 때 중요한 것은 연산자의 연산 순서다. 연산 순서에 따라 최종 계산 결과가 달라질 수 있기 때문이다.
1 + 3 / 2 식을 예로 들어보자. 덧셈을 먼저 계산하면 결과가 2지만, 나눗셈을 먼저 계산하면 결과는 2.5가 된다.
파이썬의 연산 순서는 수학과 똑같다. 왼쪽에서 오른쪽 순으로 계산하되, 곱셈과 나눗셈을 덧셈과 뺄셈보다 먼저 계산한다. 그러므로 1 + 3 / 2 식을 파이썬으로 계산하면 2.5가 된다.
코드 2-5 연산 우선 순위
>>> 1 + 3 / 2 # 나눗셈이 덧셈보다 연산 우선 순위가 높다.
2.5
연산 순서를 조정하는 방법도 수학과 같다. 먼저(그리고 독립적으로) 계산되어야 할 부분이 있다면 괄호로 둘러싼다. 1 + 3 / 2 식에서 덧셈이 먼저 계산되게 해 보자.
코드 2-6 괄호를 이용해 연산 순서 조정하기
>>> (1 + 3) / 2 # 괄호로 둘러싼 식이 먼저 계산된다
2.0
>>> (20 - 10) + (40 / (-2 - 8)) # 더 복잡한 식도 마찬가지
6.0
개념 정리
- 파이썬 코드로 수식을 작성하여 계산(평가)할 수 있다.
- 사칙 연산 기호, 괄호 등의 연산자를 사용할 수 있다.
식이 너무 길 때
식이 너무 길어지면 행바꿈을 하고 다음 행에 이어서 식을 작성하고 싶어진다. 그런데 엔터 키를 눌러 행바꿈을 하면 식이 입력한 부분까지만 계산되어 버린다. 예를 들어, 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 + 13 + 14 + 15 를 계산하는 식을 작성하다가 중간에 엔터 키를, 코드 2-7과 같이 식을 다 입력할 수 없다.
코드 2-7 식을 입력하는 도중 엔터 키를 누른 경우
>>> 1 + 2 + 3 + 4 + 5 # 엔터 키를 누르면 식이 바로 계산된다
15
괄호를 이용하면 행을 바꾸어가며 식을 입력할 수 있다. 괄호가 열린 채로 식을 입력하면, 중간에 행을 바꾸더라도 괄호를 닫기 전까지는 식이 끝나지 않는다. 괄호가 닫히면 비로소 식이 계산된다.
코드 2-8 식을 괄호로 감싸 여러 행에 걸쳐 입력하기
>>> (1 + 2 + 3 + 4 + 5 # 식을 괄호로 감싸면
... + 6 + 7 + 8 + 9 + 10 # 행을 바꿔도 계속 입력할 수 있다
... + 11 + 12 + 13 + 14
... + 15) # 괄호를 닫으면 식이 계산된다
120
대화식 셸의 연속 입력 프롬프트
파이참의 대화식 셸에서 여러 행에 걸쳐 식을 입력할 경우, 프롬프트가
...으로 변한다. 이것은 코드 입력이 다음 행에 걸쳐 계속되고 있기 때문에 코드를 마저 입력해 달라는 뜻이다. 코드를 다 입력하면(괄호를 닫으면) 프롬프트가 원래 모양(>>>)으로 바뀐다.
연습문제
2장부터는 연습문제가 제공된다. 프로그래밍은 학습은 숙달이 필요한 과정이므로 연습문제를 많이 풀어보는 것이 중요하다.
각 장에는 연습문제가 있고, 번호가 매겨져 있다. 연습문제를 풀 때는 프로그램 파일을 exercise_2_1.py와 같이 exercise_장번호_문제번호.py와 같은 형식의 파일명으로 만들자. 만든 프로그램을 실행해서 출력 결과가 올바른지도 확인해야 한다.
연습문제 2-1 수식 계산 1
다음 수식을 파이썬 프로그램으로 작성하고 계산 결과를 출력하라.
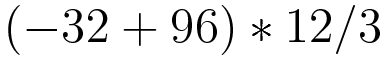
힌트: 대화식 셸은 수식 계산 결과를 자동으로 출력해준다. 하지만 프로그램 파일을 작성할 때는 출력 명령을 여러분이 직접 내려야 한다. 화면에 결과를 출력하는 방법이 기억나지 않는다면 1장을 참고하자.
연습문제 2-2 수식 계산 2
다음 수식을 파이썬 프로그램으로 작성하고 계산 결과를 출력하라.
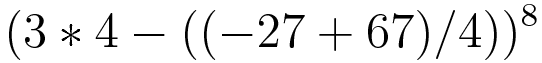
힌트: 식이 복잡해 작성하기 어렵다면 대화식 셸에 한 부분씩 입력하며 중간 결과를 확인하자.
연습문제 2-3 수식 계산 3
다음 수식을 파이썬 프로그램으로 작성하고 계산 결과를 출력하라.
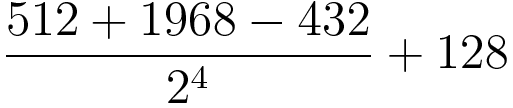
2.1.2 등식과 부등식
수학에서 등식과 부등식은 수의 크기를 비교할 때 사용된다. 파이썬에서도 등식과 부등식을 표현할 수 있고, 컴퓨터는 그 식이 참인지 거짓인지 계산해 준다. 코드 2-9은 여러 가지 등식과 부등식을 파이썬으로 나타내고 계산한 것이다. 여러분도 대화식 셸에 입력하여 계산해 보자.
코드 2-9 등식과 부등식
>>> 1+2 == 3 # 양변이 같다 (== 등호가 2개인 것에 주의)
True
>>> 1+2 != 4 # 양변이 다르다 (!=)
True
>>> 1 < 2 # 좌변이 우변보다 작다 (<)
True
>>> 1 > 2 # 좌변이 우변보다 크다 (>)
False
>>> 1 < 2 < 3 < 4 # 여러 수를 한 행에서 비교할 수도 있다
True
코드 2-9에서 보는 것처럼, 등식과 부등식의 계산 결과가 True 또는 False로 출력된다. True는 식의 계산 결과가 참임을, False는 식의 계산 결과가 거짓임을 의미한다.
==, < 처럼 등식과 부등식에서 데이터를 비교할 때 사용되는 연산자를 비교 연산자라고 부른다. 양변이 같음을 의미하는 연산자는 ==이다. 등호를 두 개 붙여 쓴다. 다음 절에서 배울 대입 연산자(=)와는 전혀 다르므로 등호 개수를 잘 구별하자. 양변이 다름을 의미하는 연산자는 !=이다. 느낌표와 등호를 붙여 쓴다. 자주 사용되니 잘 기억해 두자.
비교 연산자는 이 외에도 몇 개가 더 있다. 표 2-2를 참고하자.
| 연산자 | 의미 |
|---|---|
== |
양변이 같다 |
!= |
양변이 다르다 |
< |
좌변이 우변보다 작다 (미만) |
<= |
좌변이 우변보다 작거나 양변이 같다 (이하) |
> |
좌변이 우변보다 크다 (초과) |
>= |
좌변이 우변보다 크거나 양변이 같다 (이상) |
표 2-2 비교 연산자
비교 연산은 컴퓨터를 이용해 어떤 사실을 판단하고 조건에 따른 처리를 하는 데 중요한 역할을 한다. 이에 관해서는 4장과 5장에서 더 자세히 알아볼 것이다.
개념 정리
- 파이썬에서 등식과 부등식을 평가하면 그 식이 참인지 거짓인지
True또는False로 판단된다.
연습문제
연습문제 2-4 수식 계산 4
다음 수식을 파이썬 프로그램으로 작성하고 계산 결과를 출력하라.
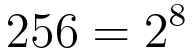
연습문제 2-5 수식 계산 5
다음 수식을 파이썬 프로그램으로 작성하고 계산 결과를 출력하라.
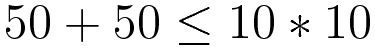
연습문제 2-6 수식 계산 6
다음 수식을 파이썬 프로그램으로 작성하고 계산 결과를 출력하라.
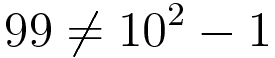
2.1.3 함수를 이용한 계산
수학에는 다양한 계산법이 있기 때문에 수식을 풀다보면 사칙연산만으로는 부족한 상황을 마주할 것이다. 덧셈·뺄셈처럼 산술 연산에 기호를 할당해 두면 좋겠지만, 할당할 수 있는 기호는 한정되어 있다. 그래서 연산자가 아닌 함수로 제공되는 연산도 많다. 이 절에서는 가장 자주 사용되는 몇 가지 수학 함수를 소개한다.
함수라고 하면 왠지 어려울 것 같지만, 사실 여러분은 함수를 이미 사용한 적이 있다. 1장에서 배운 화면에 텍스트를 출력하는 함수 print()가 그것이다. 함수를 사용할 때는 함수 이름에 괄호를 붙여 연산하려는 데이터를 넣어주면 된다. 예를 들어, print(10) 을 실행하면 화면에 10이 출력된다. 함수를 이렇게 사용한다는 것을 염두에 두고 다음 내용을 살펴보자. 계속 강조하지만, 대화식 셸에 코드를 직접 따라 입력해 보는 것이 중요하다.
절대값
abs() 함수를 사용하면 수의 절대값을 구할 수 있다. 이 함수의 이름 abs는 절대값을 의미하는 영어 용어 the absolute value에서 딴 것이다. 절대값을 구하려는 수를 괄호 안에 입력하면 된다.
코드 2-10 abs() 함수로 절대값 구하기
>>> abs(10) # 양의 정수 10의 절대값
10
>>> abs(-10) # 음의 정수 -10의 절대값
10
소수 반올림
소수를 반올림할 때는 round() 함수를 사용한다. round는 반올림을 뜻하는 영어 용어 round off에서 딴 이름이다. 반올림 위치를 지정하려면 round(수, 자릿수)와 같이 콤마(,) 뒤에 반올림 위치의 수를 적어준다. 자리수를 지정하지 않으면 정수로 반올림된다. 다음 코드를 대화식 셸에 입력해 보자.
코드 2-11 round() 함수로 소수 반올림
>>> round(3.141527) # 소수를 정수로 반올림
3
>>> round(3.141527, 2) # 소수점 둘째 자리까지 반올림
3.14
>>> round(3.141527, 4) # 소수점 넷째 자리까지 반올림
3.1415
>>> round(10 / 6) # 10 / 6(1.66...)을 정수로 반올림
2
제곱근
abs() 함수와 round() 함수는 파이썬의 기본 내장 함수다. 그 외의 여러 가지 수학 함수는 math 모듈에 묶여 제공된다. math 모듈의 함수를 사용하기 위해서는 먼저 import math 명령을 실행하여 math 모듈을 임포트해 두어야 한다.
내장 함수와 추가 모듈의 함수
내장 함수는 파이썬에서 가장 자주 사용되는 기본 함수로, 별도로 추가 기능을 불러오지 않아도 언제나 사용할 수 있다. 내장 함수로는
print(),input(),abs(),round()등 여러 가지가 있다.그 외의 함수들은 서로 관련된 것끼리 모듈(미리 만들어 둔 코드 묶음)에 담겨 제공된다. 모듈로 제공되는 함수를 사용하려면 import 문으로 모듈을 임포트(프로그램 외부의 모듈을 프로그램 속에서 사용할 수 있게 불러들이는 것)해야 한다. 모듈을 한 번 임포트해 두면 그 프로그램이 종료될 때까지 계속 사용할 수 있다.
모듈과 import 문에 관해서는 10장에서 자세히 배울 것이다. 지금은
math모듈에 포함된 함수(math.으로 시작되는 함수)를 사용하려면import math를 먼저 실행해야 한다는 것만 기억하자.
math.sqrt() 함수를 이용하면 수의 제곱근을 구할 수 있다. ‘sqrt’라는 이름은 제곱근을 뜻하는 영어 단어 ‘square root’에서 딴 것이다. 이 함수는 math 모듈에 포함된 함수이므로, 사용하기 전 import math를 먼저 실행해야 한다. 다음은 2와 9의 제곱근을 구하는 예다.
코드 2-12 math.sqrt() 함수로 제곱근 구하기
>>> import math # math 모듈을 임포트한다
>>> math.sqrt(2) # 2의 제곱근
1.4142135623730951
>>> math.sqrt(9) # 9의 제곱근
3.0
이상으로 자주 쓰이는 수학 함수 몇 가지를 살펴보았다. 다음과 같이 정리해 두자.
알아두기
abs()함수: 수의 절대값을 구한다.round()함수: 소수를 반올림한 수를 구한다.math.sqrt()함수: 수의 제곱근을 구한다.math.으로 시작하는 함수를 사용하기 전,import math를 실행해 두어야 한다.
연습문제
연습문제 2-7 수식 계산 7
다음 수식을 파이썬 프로그램으로 작성하고 계산 결과를 출력하라.
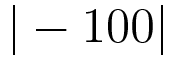
연습문제 2-8 수식 계산 8
다음 수식을 소수점 둘째 자리까지만 계산하여 파이썬 프로그램으로 출력하라.
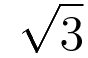
힌트: 반올림은 round() 함수를 이용하고, 자리수를 지정하려면 round(수, 자리수)와 같은 형태로 지정한다.
2.1.4 수식을 응용한 문제
현실의 문제는 수식으로 제공되지 않는다
프로그래머가 해결해야 하는 현실의 문제는 수식의 형태로 제공되지 않는다. 여러분은 “100 / 3” 이라는 수식 대신 “학생 100명을 3개의 학급에 균등하게 나누어 주세요” 라는 요청을 받을 것이다. 이런 문제는 수식과는 달리 컴퓨터 프로그램으로 간단히 옮길 수가 없다. 컴퓨터는 사람의 말과 생각을 이해하지 못하기 때문이다.
수식이 아니라 사람의 말(자연어)로 주어진 문제를 해결하려면, 여러분이 문제에서 다루어야 할 수와 데이터를 추려내고, 그 처리 방법을 수식과 프로그램으로 작성할 수 있어야 한다. 문제에서 수식을 찾아내는 것이 항상 쉬운 것은 아니지만, 많이 연습하면 익숙해질 것이다. 간단한 문제를 하나 살펴보자.
연오는 자취방을 구하고 있다. 열심히 발품을 팔며 조사한 끝에 가장 마음에 드는 방 두 개를 찾았다.
- 방 A는 가로 2.5m, 세로 3m이고, 월세 27만원이다.
- 방 B는 가로 4m, 세로 2m이고, 월세 30만원이다.
어느 방이 가격 대비 더 넓은가?
이 문제는 컴퓨터가 이해할 수 없는 언어로 작성되어 있다. 프로그래머가 직접 문제를 해석하여 수식을 작성해야 풀 수 있다. 다행히 문제가 명확하게 정의되어 있고, 문제를 해결하는 방법도 간단하다. 직각사각형의 넓이를 구하는 식(가로길이 * 세로길이)만 알면 다음과 같이 쉽게 비교식을 만들 수 있다.
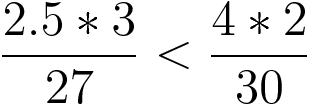
이 식을 계산한 결과가 참이라면 가격대비 방 B가 더 넓은 것이고, 거짓이라면 방 A가 더 넓은 것이다. 이 식을 직접 계산한다면 골치가 아프지 않겠는가? 수식을 코드로 옮겨 실행하면 컴퓨터가 계산을 대신해주니 결과를 보기만하면 된다.
이 수식을 대화식 셸에 입력해 계산해 보자.
코드 2-13 두 방의 넓이 비교
>>> (2.5 * 3 / 27) < (4 * 2 / 30)
False
계산 결과가 거짓이므로, 방 A가 가격대비 더 넓다는 것을 알 수 있다. 이렇게 현실의 문제를 해결할 때는 먼저 수식으로 나타낸 뒤, 프로그램으로 옮겨 계산하면 된다.
실제 문제를 다룰 때 필요한 도메인 지식
파이썬 문법을 잘 아는 것만으로는 모든 문제를 해결할 수 없다. 앞에서 다룬 방 넓이를 비교하는 문제만 생각해 봐도, 직사각형의 넓이를 구하는 방법을 모른다면 프로그램을 작성하기 어려울 것이다. 좀 더 복잡하고 어려운 현실의 문제를 해결할 때는 더 많은 지식이 필요할 것이다. 다음 문제를 살펴보자.
주식회사 파이중공업은 한 해 동안 철강, 석유 등의 원자재(불변자본)를 구매하는 데 30억 원을, 노동자를 고용(가변자본)하는 데 15억 원을 사용했다. 파이중공업은 이를 통해 선박을 제조·판매하여 45억 원의 순수익(잉여가치)을 냈다.
파이중공업의 한 해 이윤율은 얼마인가?
이 문제도 프로그래머가 문제를 해석하여 수식을 작성해야 한다. 하지만 이윤율을 어떻게 구할 수 있는지 알고 있는가? 문제 해결을 요청한 사람은 해당 분야의 지식을 당연하게 여겨 특별한 언급을 하지 않았지만 프로그래머에게는 그런 지식이 없을 수도 있다.
이처럼 프로그래밍 기술보다는 문제 자체와 관련된 지식을 도메인 지식(domain knowledge)이라고 한다. 문제 해결에 필요한 도메인 지식을 알지 못할 때는 문제 해결을 요청한 당사자에게 정보를 요구하거나 직접 지식을 조사해야 한다.
이 문제 같은 경우는, 위키백과에서 ‘이윤율’을 검색해 보면 힌트를 얻을 수 있다. ‘이윤율의 경향적 저하 법칙’이라는 문서에 이윤율 공식이 다음과 같이 나와 있다.
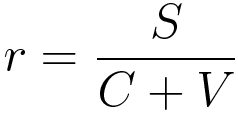
r이 이윤율, C가 불변자본, V가 가변자본, S가 잉여가치액이므로, 이 문제는 다음과 같이 계산할 수 있다.
코드 2-14 파이중공업의 이윤율 계산
>>> 45 / (30 + 15)
1.0
파이중공업의 이윤율은 1.0이다.
연습문제
필요한 지식을 구하고 수식을 이끌어내어, 현실의 문제를 해결하는 프로그램을 작성해 보자.
연습문제 2-9 환율 계산
한국에 사는 여러분은 외국 인터넷 쇼핑몰에서 노트북을 구매하려 한다. 이 쇼핑몰에서는 달러(USD) 또는 유로(EUR)로 결제할 수 있고, 노트북의 가격은 780 달러 또는 650 유로다. 달러로 사는 것과 유로로 사는 것 중 어느 쪽이 더 저렴한가? 파이썬 프로그램을 작성하여 해결해 보아라.
힌트: 이 문제에서 필요한 지식은 달러와 유로의 가격(환율)이다. 현재 환율을 인터넷에서 검색해 보자. 환율은 매일 바뀌니 문제를 푸는 시기에 따라 답이 다를 수 있다.
연습문제 2-10 원형 운동장
어느 학교의 운동장은 원형이고 지름이 100m다. 운동장의 가장자리에 바깥쪽 트랙이 있고, 그 트랙에서 5m 안쪽에 안쪽 트랙이 있다. 이 운동장에서 두 선수가 나란히 운동장을 한 바퀴 달리는 시합을 하려 한다. 두 선수가 달리는 거리를 서로 같게 하려면 안쪽 트랙에서 달리는 선수가 바깥쪽 트랙에서 달리는 선수보다 몇 미터 더 달려야 하는가? 파이썬 프로그램을 작성하여 해결해 보아라.
댓글 남기기